カイ二乗(χ2)検定(カイじじょうけんてい)は、帰無仮説が正しければ検定統計量がカイ二乗分布に従うような統計学的検定法の総称である。次のようなものが含まれる。
これらはいずれも

(ここで"expected" という語は期待値そのものではなく観測値から求められる期待値の推定量あるいは理論値を指すことが多い)
という形の統計量「カイ二乗(χ2)」を含む。

である。ただしここでO= 頻度の観測値、E= 帰無仮説から導かれる頻度の期待値(理論値)である。
ピアソンのカイ二乗検定は2つのタイプの比較、適合度検定および独立性検定に用いられる:
観測された頻度分布が理論分布と同じかどうかを検定する。たとえば簡単な例として、標本として100人の人がいる場合に、「男と女が同数だけいる集団から、ランダムに抽出された100人である」という仮説を検定するには、男女の人数の観測値と理論値(50:50)とを比較すればよい。観測値が男45人、女55人ならば、
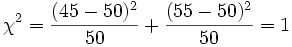
この場合の自由度は1である(2つの観測値と理論値の差は、一方がわかればもう一方もわかるから)。そこで自由度1のカイ二乗分布をみると、男女の人数が等しい場合にこのような差(および女がさらに多くなるような場合)が見出される確率は、約0.3である。この確率は普通用いる統計学的有意水準(0.05、0.01など)よりも高いから、「男女の人数が等しい」とする帰無仮説は認めてよい。
2つの変数に対する2つの観察(2x2分割表で表される)が互いに独立かどうかを検定する。たとえば、「別の地域の人々について、選挙である候補を支持する頻度が違う」かどうかを検定する方法である。
カイ二乗の計算値は、確率分布が二項分布あるいは正規分布に従う集団に関しては正確にカイ二乗分布に従う。
(ただしここで、p= 帰無仮説のもとでの確率、n= 標本の観測値) に従う場合、カイ二乗は自由度1のカイ二乗分布に従う。なおこの二項分布は標本数が大きい場合には次のような正規分布で近似できる:
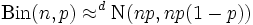

に従う。
しかし一般の頻度分布でもカイ二乗は近似的にはカイ二乗分布に従うので、カイ二乗検定が適用可能である。期待値Eが小さい(標本数が小さい、または観測数が少ない)場合は、二項分布を正規分布ではうまく近似できないため、この場合には尤度比検定の1つであるG検定を用いるのがより適切である。全標本数が小さい場合は、二項検定、さらに2x2分割表で表される場合にはフィッシャーの正確確率検定を用いる必要がある。
| お店 | ポテト | チキン | 合計 |
|---|---|---|---|
| ワクドナルドW | 435 | 165 | 600 |
| ボスバーガー B | 265 | 135 | 400 |
この表によると、Wのチキンの売り上げは165個で、それに対してBのチキンの売り上げは135個でした。しかし、このチキンの売り上げ数だけを単純に比べても、両店で違いがあるかどうかは分かりません。なぜなら、両店の全体の売り上げ数が違うからです。そこで、ハンバーガーショップの定番商品であるポテトの売り上げ数を基準にして比べることにします。
これで見る限り、Bの方がチキンの売り上げの割合が多そうに思えます。
さて、これだけで、「Bの方がチキンの売り上げが、割合として多い」と断言していいのでしょうか。統計学では、これをどのように考えるのでしょうか。
統計学では、まず「仮説」を立てるところから出発します。仮説とは、「○○である」ということを仮に立てたものです。そのあとで、それを肯定するか、あるいは否定するかを決めるのです。
ここでは、次の仮説を立ててみました。
「チキンとポテトの売り上げの割合に関して、WとBの間に差はない」
おや「……差はない」ですか。これはどういうことでしょうか。ふつうは、「差がある」ことを証明したいわけですから、「差はある」という仮説を立てるのが自然ではないでしょうか。
その通りです。しかし、統計学では、あえて「差はない」という仮説を最初に立てます。これを「帰無仮説」と呼びます。
なぜ帰無仮説を最初に立てるかというと、「差はある」という仮説は、「大きな差がある」、「小さな差がある」、「中位の差がある」などなど、無限に立てられるからです。そのひとつひとつについて検討するのは事実上不可能です。それに対して、帰無仮説「差はない」というのは、これ以外の形はありません。ですから、これを肯定するか、否定するかを決めればいいことになり、単純になります。
仮説を肯定することを「採択する」、否定することを「棄却する」といいます。
もし帰無仮説が採択されれば、「差はない」と結論します。反対に、もし帰無仮説が棄却された場合は、「差はない、とは言えない」つまり「差はある」と結論されることになります。帰無仮説の反対の仮説のことを、「対立仮説」と呼びます。対立仮説は、帰無仮説が棄却されたときに採択される仮説で、「差はないとは言えない、つまり差はある」という形です。
まとめると、次のような流れになります。
帰無仮説として「売り上げの割合に差はない」という仮説を立てます。WもBも、ポテトとチキンがまったく同じ割合で売れるとしたときの、売り上げ個数をだしてみましょう。そこで、帰無仮説による個数と実際の個数がそれほど変わらなければ、帰無仮説を採択し、差はないと結論することになります。
両店で、ポテトとチキンが同じ割合で売れるとしたときの個数を計算します。それぞれのお店の売り上げ個数と、ポテトとチキンの売り上げ個数を使えば、その個数を求めることができます。
| お店 | ポテト | チキン | 合計 |
|---|---|---|---|
| W | ? | ? | 600 |
| B | ? | ? | 400 |
| 合計 | 700 | 300 | 1000 |
上の表のように合計個数だけをみると、全体の売り上げに対して、それぞれのお店の合計個数の割合は、
それに対して、ポテトとチキンの割合は700対300です。
ですから、同じ割合で売れるとしたら、
それでは、チキンの個数はどれくらいになるでしょうか。計算して、下の表を埋めてください。
| お店 | ポテト | チキン | 合計 |
|---|---|---|---|
| W | 420 | 600 | |
| B | 280 | 400 | |
| 合計 | 700 | 300 | 1000 |
どうなりましたか。
結局、同じ割合で売れるとしたときの売り上げ個数の表は下のようになります。
| お店 | ポテト | チキン | 合計 |
|---|---|---|---|
| ワクワク | 420 | 180 | 600 |
| モグモグ | 280 | 120 | 400 |
| 合計 | 700 | 300 | 1000 |
この個数を「期待度数」と呼びます。これは、帰無仮説、つまり「両店のポテトとチキンの売り上げ割合に差がない」が成立したときに、期待される度数ということです。
しかし、実際の売り上げ個数はこのようになっていました。
| お店 | ポテト | チキン | 合計 |
|---|---|---|---|
| ワクワク | 435 | 165 | 600 |
| モグモグ | 265 | 135 | 400 |
| 合計 | 700 | 300 | 1000 |
この個数を「観測度数」と呼びます。つまり、実際に観測された度数ということです。
観測度数と期待度数とを比較してみると、次のことが言えます。
さて、このように期待度数と観測度数には違いがあることがわかりました。しかし、はたしてこの違いには「意味があるのでしょうか」? たとえば、Wのポテトの個数は、観測度数435に対して、期待度数は420でした。この435と420との差「15」には意味があるのかどうか?
「意味があるのかどうか」ということは、こういうことです。たとえば、460と420というデータがあって、この2つのずれは、本来同じだったのにたまたまずれてしまったものなのか、あるいは、本来違っているものが現れてきたものなのか、このどちらなのかを決めるということです。
さらに言い換えれば、このずれは「誤差の範囲内のもの」なのか、それとも「誤差とは言えない、誤差以上のもの」なのか、を決めるということです。
これを決めるためには、検定という考え方を知る必要があります。
さて、ポテトとチキンの売り上げから
| お店 | ポテト | チキン | 合計 |
|---|---|---|---|
| W | 435/420 | 165/180 | 600 |
|
B |
265/280 | 135/120 | 400 |
| 合計 | 700 | 300 | 1000 |
このカイ2乗値は、
(((観測度数-期待度数)の2乗)÷期待度数)の総和
(435-420)^2/420+(165-180)^2/180+(265-280)^2/280+(135-120)^2/120
=15^2/420+(-15)^2/180+(-15)^2/280+15^2/120
=0.536+1.250+0.804+1.875
=4.46 (小数点第3位を四捨五入)
この値はカイ2乗分布にしたがっているわけですが、自由度はいくつになるのでしょうか。
この場合は、
これらをかけ算して、1×1=1。自由度は1になります。
この意味は、「Wのポテトが決まると、Wのチキンが決まり(合計が決まっているから)、同時に、Bのポテトが決まり(合計が決まっているから)、さらにそれによって、Bのチキンも決まる。ということは、1つの値が決まれば、残りは自動的にきまる。つまり自由度は1である」ということです。
一般的に、行と列がある二次元の表の場合は、
自由度=(行の数-1)×(列の数-1)
となります。
さて、自由度は1、カイ2乗値は4.46となりました。この値は大きいのでしょうか、小さいのでしょうか。言い換えれば、確率的に起こりにくいことなのでしょうか、起こりやすいことなのでしょうか。
自由度とカイ2乗値がわかったときに、それが起こる確率を調べる必要があります。そのときに、カイ2乗分布表を使うと便利です。
| ↓自由度/確率→ | 0.05 | 0.01 |
|---|---|---|
| 1 | 3.84 | 6.63 |
| 2 | 5.99 | 9.21 |
| 3 | 7.81 | 11.34 |
| 4 | 9.49 | 13.28 |
| 5 | 11.07 | 15.09 |
| …以下続く… | … | … |
いま、自由度1のカイ2乗分布を考えると、次のようなグラフになります。

カイ2乗値が3.84のところでグラフを区切ると、それよりも左側で0.95(95%)、それよりも右側で0.05(5%)の面積になります。つまり、カイ2乗値が3.84よりも小さい値は、95%の確率で起こります。また、カイ2乗値が3.84よりも大きい値は、5%の確率でしか起こらないということになります。
つまり「WとBではポテトとチキンの売り上げの割合には差がない(帰無仮説)」としたときに、そのカイ2乗値が3.84よりも大きくなる確率は5%よりも小さいということです。
さらにカイ2乗値が6.63よりも大きくなる確率は、1%よりも小さくなります。
さて、計算したカイ2乗値は4.46でした。これは次のように解釈できます。「WとBのお店によってポテトとチキンの売り上げの割合には差がない(帰無仮説)」としたときに、そのカイ2乗値が4.46をとる確率は、5%よりも小さく、1%よりも大きい。
カイ2乗値4.46がでてくる確率は、1%から5%の間だということがわかりました。これは、100回やって1回から5回しか起こらないということです。これは「起こりにくい」とするべきでしょうか。それとも「それほど起こりにくいことではない」とするべきなのでしょうか。確かに宝くじの一等が当たる確率よりは、大きいのですが。
めったに起こらないか、そうではないか、を決めるのに、統計学では「有意水準」というものを使います。有意水準よりも小さい確率であれば、それは「めったに起こらないこと」、つまり、偶然の誤差ではないと認定します。有意水準よりも大きい確率であれば、「めったに起こらないこととはいえない」、つまり、偶然の誤差であるとします。
有意水準は伝統的に、5%か、あるいは1%を使います。有意水準5%よりも、有意水準1%の方が厳しい判断の仕方といえます。5%、1%どちらを有意水準として使ってもかまいません。重要なのは、あらかじめ有意水準を決めておくということです。
さて、話をチキンとポテトに戻しましょう。
カイ2乗値は4.46でした。これは、5%から1%の確率で起こることです。
ここで、有意水準として5%をとるとすると、それよりも小さい確率ですので、「めったに起こらないこと」と認定できます。これは次のように解釈できます。
カイ2乗検定の結果「WとBではポテトとチキン売り上げの割合に差がある」という結論が得られました。
あなたはこの結論を店員さんに知らせました。
「ポテトとチキンの売り上げについてカイ2乗検定をしたんですよ」
「な、なんだい、そのカイなんとかというのは?」